Tutto l’apprendimento delle reti neurali moderne si fonda sulla discesa del gradiente.
Pensate che l’idea di questo algoritmo risale al 1800, ma solo negli anni ’80 è stata riscoperta grazie alla backpropagation.
C’è stata una fase buia nell’intelligenza artificiale, denominata “la seconda era glaciale” (vedi post omonimo), quando, dopo le critiche di Minsky e Papert al Perceptron, sembrava che le reti neurali si dovessero accantonare per sempre.
Poi, nel 1986, Rumelhart, Hinton e Williams hanno trovato un modo per aggiornare i pesi negli strati nascosti e hanno dato vita al cosiddetto “disgelo” delle reti neurali.
Il deep learning, così come lo conosciamo oggi – capace di interpretare immagini e testo – è esploso solo quando è stato possibile combinare hardware potente, montagne di dati e versioni migliorate della discesa del gradiente.
La cosa bella di questo algoritmo è che funziona secondo una logica semplicissima:
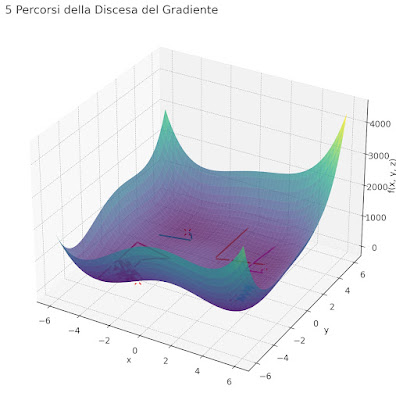
Dal grafico si possono scorgere le traiettorie che l’algoritmo percorre: alcune finiscono in minimi locali (come gli alpeggi o le radure vallive), mentre solo una scende nella vallata più bassa, il minimo globale.
Semplice ma geniale: è questa semplicità che ha permesso al deep learning di conquistare il mondo
La funzione dello script Python, in realtà, è un “assemblato”.
La prima parte:
Pensate che l’idea di questo algoritmo risale al 1800, ma solo negli anni ’80 è stata riscoperta grazie alla backpropagation.
C’è stata una fase buia nell’intelligenza artificiale, denominata “la seconda era glaciale” (vedi post omonimo), quando, dopo le critiche di Minsky e Papert al Perceptron, sembrava che le reti neurali si dovessero accantonare per sempre.
Poi, nel 1986, Rumelhart, Hinton e Williams hanno trovato un modo per aggiornare i pesi negli strati nascosti e hanno dato vita al cosiddetto “disgelo” delle reti neurali.
Il deep learning, così come lo conosciamo oggi – capace di interpretare immagini e testo – è esploso solo quando è stato possibile combinare hardware potente, montagne di dati e versioni migliorate della discesa del gradiente.
La cosa bella di questo algoritmo è che funziona secondo una logica semplicissima:
- Definisci cosa vuoi minimizzare (funzione di costo).
- Calcola il gradiente (la direzione della massima pendenza).
- Aggiorna i pesi andando nella direzione opposta.
- Ripeti finché non converge.
Dal grafico si possono scorgere le traiettorie che l’algoritmo percorre: alcune finiscono in minimi locali (come gli alpeggi o le radure vallive), mentre solo una scende nella vallata più bassa, il minimo globale.
Semplice ma geniale: è questa semplicità che ha permesso al deep learning di conquistare il mondo
La funzione dello script Python, in realtà, è un “assemblato”.
La prima parte:
\( f(x, y) = 2[(x^2 + y - 11)^2 + (x + y^2 - 7)^2] \)
è la ben nota funzione di Himmelblau, usata spesso per testare algoritmi di ottimizzazione perché ha più minimi locali, che qui ho esteso al 3D con l’aggiunta di un termine quadratico centrato in z = 3 (il fattore 5 rende la parabola più stretta in modo da guidare la discesa):\( f(z) = 5(z - 3)^2 \)
Il gradiente diventa:
\[
\nabla f(x, y, z) =
\begin{bmatrix}
2 \left[4x(x^2 + y - 11) + 2(x + y^2 - 7)\right] \\
2 \left[2(x^2 + y - 11) + 4y(x + y^2 - 7)\right] \\
10(z - 3)
\end{bmatrix}
\]L’applicazione dell’algoritmo di discesa del gradiente trova correttamente il punto più basso “programmato” della funzione:
- Minimo trovato: [-2.805, 3.131, 3.0]
- Valore della funzione: praticamente 0
Il grafico mostra in modo più marcato il minimo globale e il cammino che conduce ad esso.
Promemoria
Formula generale per l’aggiornamento dei pesi (discesa del gradiente):
\[
w_{ij} := w_{ij} - \eta \cdot \frac{\partial E}{\partial w_{ij}}
\]
In una rete neurale semplice, la derivata può essere calcolata come:\[ \frac{\partial E}{\partial w_{ij}} = \delta_j \cdot o_i \] Dove \[ o_i\] è l'output del neurone.
E\[\delta_j\] l'errore nel caso di un neurone con funzione di attivazione g, è:
\[ \delta_j = (t_j - y_j) \cdot g'(h_j) \]